Tare conexitate
Un graf orientat G=(V,E) este tare conex dacă pentru orice pereche de noduri distincte (x,y) există cel puțin un drum de la x la y și există cel puțin un drum de la y la x.
Pentru un graf orientat, se numește componentă tare conexă un subgraf tare conex maximal - prin adăugarea a încă unui nod, subgraful obținut nu mai este tare conex.
Exemplu

Graful de mai sus nu este tare conex. El are trei componente tare conexe.
Verificarea tare conexității. Determinarea componentelor tare conexe
Verificare tare conexității unui graf orientat poate fi privită ca un caz particular al determinării componentelor tare conexe, deoarece, dacă graful are o singură componentă tare conexă atunci el este tare conex. În continuare vom vedea două metode de determinare a componentelor tare conexe. Ambele folosesc noțiunea de graf transpus, pe care o definim în continuare:
Definiție: Fie G=(V,E) un graf orientat. Se numește graf transpus al lui G graful orientat GT=(V,ET), cu aceleași mulțimea a nodurilor și pentru orice pereche de noduri are loc: (x,y) este arc în G dacă și numai dacă (y,x) este arc în GT.
Exemplu

Graf orientat inițial

Graful orientat transpus
Să observăm că pentru două noduri oarecare x, y:
- existența unui drum de la x la y poate fi determinată cu o parcurgere (de exemplu în adâncime) în graful G, pornind din nodul x;
- existența unui drum de la y la x poate fi determinată cu o parcurgere în graful GT, pornind tot din nodul x.
Algoritmul Plus-Minus
Folosind observații de mai sus, pentru a determina componentele tare conexe folosim următorul algoritm, numit Plus-Minus:
- pentru fiecare nod x al grafului care încă nu a fost plasat într-o componentă tare conexă:
- determinăm toate nodurile în care se poate ajunge din x, folosind graful G și le marcăm într-un tablou cu plus;
- determinăm toate nodurile din care se poate ajunge în x, folosind graful GT și le marcăm într-un tablou cu minus;
- nodurile marcate atât cu plus, cât și cu minus, împreună cu x formează o componentă tare conexă;
Exemplu:
Fie graful de mai sus. Să determinăm componenta tare conexă din care face parte nodul 6:

Graful inițial
S-au marcat cu plus nodurile: 5 7 8
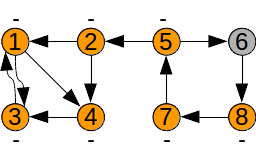
Graful transpus
S-au marcat cu minus nodurile: 1 2 3 4 5 7 8
Nodurile marcate de două ori, 5 7 8, împreună cu nodul inițial, 6, formează o componentă tare conexă.
Secvență C++:
- n, a[][] - numărul de noduri și matricea de adiacență
- nrc - numărul de componente tare conexe
- ctc[] - tablou pentru memorarea componentelor tare conexe: ctc[i] = numărul de ordine al componentei din care face parte nodul i
- s[], p[] - tablouri pentru marcare nodurilor vizitate în timpul parcurgerilor
- să observăm că graful inițial și cel transpus pot fi memorate prin aceeași matrice de adiacență
void df1(int x)
{
s[x] = 1;
for(int i =1 ; i <= n ; i ++)
if(s[i] == 0 && a[x][i] == 1)
df1(i);
}
void df2(int x)
{
p[x] = 1;
for(int i =1 ; i <= n ; i ++)
if(p[i] == 0 && a[i][x] == 1)
df2(i);
}
int main()
{
.....
for(int i = 1 ; i <= n ; ++i)
if(ctc[i] == 0)
{
for(int j = 1; j <= n ; ++j)
s[j] = p[j] = 0;
nrc ++;
df1(i); df2(i);
for(int j = 1; j <= n ; ++j)
if(s[j] == 1 && p[j] == 1)
ctc[j] = nrc;
}
....
}
Algoritmul lui Kosaraju
Alt algoritm, mai eficient, pentru determinarea componentelor tare conexe este Algoritmul lui Kosaraju.
Să ne amintim că la parcurgerea în adâncime se pot asocia nodurilor două momente de timp:
- d[x] - momentul când nodul x este descoperit și adăugat pe stivă: timpul de descoperire a nodului
- f[x] - momentul când se termină de vizitat succesorii lui x, iar nodul x se elimină de pe stivă: timpul de finalizare a nodului
Aceste momente de timp vor fi numere naturale între 1 și 2*n, unde n este numărul de noduri din graf.
Algoritmul lui Kosaraju este:
- determinăm graful transpus GT
- parcurgem în adâncime graful și determinăm pentru fiecare nod x timpul de finalizare f[x]
- parcurgem în adâncime graful transpus GT, dar considerăm nodurile în ordinea descrescătoarea timpilor de finalizare
- nodurile din arborii de parcurgere obținuți reprezintă câte o componentă tare conexă
Exemplu:

Graf orientat inițial

Graful orientat transpus

În urma parcurgerii în adâncime a grafului inițial G nodurile în ordinea finalizării sunt:
Parcurgem graful transpus GT analizând nodurile în ordinea inversă a timpilor de finalizare:
- începem cu nodul 1; se vizitează nodurile 3 4; se determină componenta tare conexă {1,3,4};
- continuăm cu nodul 2 (nodurile 1, 3 și 4 au fost vizitate mai devreme); nu se vizitează alte noduri; se determină componenta tare conexă {2};
- continuăm cu nodul 5; se vizitează nodurile 6 8 7; se determină componenta tare conexă {5, 6, 7, 8}.

Secvență C++:
#include <iostream>
using namespace std;
int a[101][101],n,succ[101],pred[101],ctc[101],nrctc,m,x,y;
void DFS1(int x)
{
succ[x]=1;
for(int i=1; i<=n; i++)
if(a[x][i]==1&&succ[i]==0)
DFS1(i);
}
void DFS2(int x)
{
pred[x]=1;
for(int i=1; i<=n; i++)
if(a[i][x]&&!pred[i])
DFS2(i);
}
void componente()
{
for(int i=1; i<=n; i++)
if(ctc[i]==0)
{
DFS1(i);
DFS2(i);
nrctc++;
for(int j=1; j<=n; j++)
{
if(succ[j]&&pred[j])
ctc[j]=nrctc;
succ[j]=pred[j]=0;
}
}
}
int main()
{cin>>n>>m;
for(int i=1;i<=m;i++)
{cin>>x>>y;
a[x][y]=1;
}
componente();
cout<<nrctc;
return 0;
}
Probleme ataşate
#0583 - Tare conexitate